本研究では流体数学の分野で卓越した実績をもつ数学者のグループと第一線の流体力学者のグループとの協働で，その複雑さ故に数学的性質が未だ完全に解明されていない流体工学の未解決問題に挑戦する．流体の複雑な運動はいたるところに見られるが，その複雑さの源は自発的・不可避的に乱れが生じることと自由に動く界面を有することにあると考えられる（Leonardo da Vinciのスケッチにも滑らかな流れが水面に注ぎ込むことによって複雑な運動が生じる様子が描かれている）．前者の代表がReynoldsの実験(注1)以来流体力学における中心課題の一つである層流から乱流への遷移現象であり，後者の代表が未だ正確なモデル化を拒み続けている混相流(注2)である．本研究では，これらについて数学的に厳密な定式化と解の挙動の解析手法を開発し，それを用いて近年環境問題化している空力騒音の発生メカニズムの解明，省エネルギー化に向けた空力抵抗削減の鍵である境界層乱流遷移制御技術の確立，さらには微細加工・洗浄あるいは先端医療への応用が注目されている高速水噴流などの複雑な混相流の現象解明を目指す．
図１　複雑な流体運動
（Leonardo da Vinciのスケッチ）


(a) von Kármán渦列

(b) 翼面上の境界層

図２　非平行流れの例		 　層流から乱流への遷移は，数学的には流れを支配する偏微分方程式の解の安定性として表現される．流体力学における流れの安定性の研究は，１９世紀後半のHelmholtz, Rayleigh, Kelvin, Reynolds以来，その重要性からTaylor，Heisenbergなど時代を代表する科学者等により活発な研究が行われてきた．その結果，近年の絶対不安定/対流不安定の理論(注3)，有限撹乱の過渡成長に関する理論(注4)も含めて，平行流れ(注5)の線型安定性に関してはほぼ完全な数学理論が完成しつつある．一方，現実の流れ場はほとんどが非平行流れであるが，その安定性を支配する数学理論は未だ完成にはほど遠い状態にある．流れの安定性の研究で用いられている数学はほとんどが古典数学の範疇であり，現在の数学研究の成果を直接反映する研究は稀である．本研究では，現代数学解析を専門とする数学者が第一線の流体研究者と協働して“流れの安定性”という流体力学の基本問題に取り組み，非平行流れを含む流れの安定性の一般的な数学理論の確立を目指す．これは流体力学の研究にこれまでにないインパクトを与えるものであるとともに，数学研究においても直接関係する変数係数偏微分方程式の漸近解析手法の発展に加え，例えば“乱れを表す数学，乱れを制御する数学”と呼べるような斬新かつ有望な研究対象を，第一線の流体力学研究のアイデアの中から見出すことができるものと期待することができる．

　また，混相流は非線型性が強く様々な長さスケール・時間スケールが混在する非常に複雑な現象であるが，その工業上の重要性から古くから様々な分野で活発な研究が行われてきた．膨大な実験データを流動様式(注6)で整理する形で様々な経験式が考案され個々のケースで活用されてきたが，その適用範囲と信頼性は限られており汎用的かつ高精度の解析手法が切望されている．近年の計算機性能の著しい発達により保存法則に基づく３次元シミュレーション(注7)が可能になってきたが，複雑な構成方程式(注8)の信頼性などについて疑問も多く，装置設計などへの応用への道のりは遥かに遠いのが現状である．本研究では，現代数学解析を駆使することによって混相流の素過程に対して数学的に正しいモデル化・定式化を開発し，この状況を打開することを目指す．特に，分子レベルのミクロスコピックな視点と連続体極限からの非平衡統計力学による流体力学へのアプローチを導入し，新たなモデル化・定式化を試みる．これにより現在の枠を超えた次世代の混相流シミュレーション技術の確立に寄与することができる．同時に，複雑な混相流のモデル化・定式化の過程では今までにない解析手法が必要になることが考えられ，流体研究者から提供される知見を基に例えば“界面を表す数学，界面を制御する数学”と呼べるような新たな数学解析・数学理論へのきっかけが得られると期待することができる．
(a) 水撃による管内気泡の生成消滅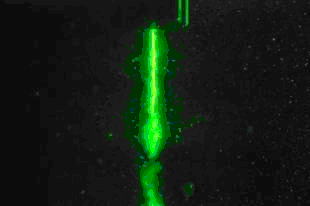

(b) キャビテーションジェット
図３　複雑な混相流の例
　なお，流体工学の分野には層流－乱流遷移現象と混相流の他にも数学的に厳密な理論の構築が待たれている分野が数多く存在する．本研究により数学解析の研究者と流体力学の研究者の相互理解が進み，将来的にそれらの分野にも数学的な研究が波及することが期待できる．Euler, LagrangeからCauchy, Stokesまで流体力学と数学解析は緊密な関係をもって発展してきた．本研究によってこれらを現代のレベルで再び結び付ける端緒を与えることができると考える．





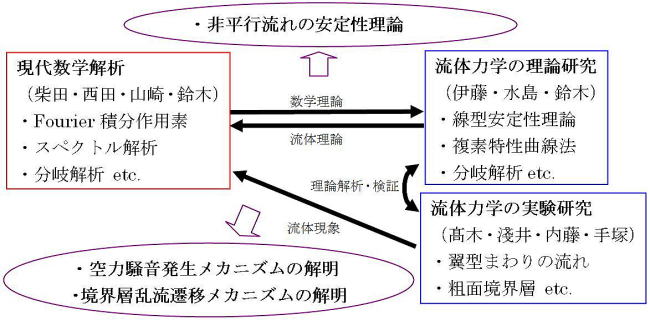
図４ 流れの安定性研究の進め方




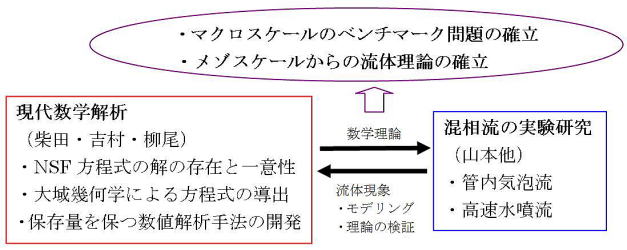
図５　混相流研究の進め方
　　　
(from HP of School of Math., Univ. Southampton)
（注6）
　時間・空間平均した方程式は、必然的に平均したことにより失われた微細構造の影響を表す項を含む。その項を評価するためには何らかのモデル化が必要であり、それを構成方程式と呼ぶ。
（注7）
　ただし、複雑な混相流において相界面の運動と各相の支配方程式を厳密に連成させて計算することは、現在の計算機能力をもってしても不可能である。その場合、それらを時間・空間平均した方程式を解くことによりシミュレーションが行われている。


気泡流　　　スラグ流　　　チャーン流　　環状噴霧流
（注6）
　流れを各相が占める幾何的な様相によって分類したものを流動様式と呼ぶ。鉛直管内の気液二相流の場合は例えば下図に示すようなものが挙げられる。
（注5）
　流れが流れ方向には変化せず流れを横切る１方向のみ変化する場合を平行流という。厳密な平行流はCuette流、Poiseuille流などの極端に単純な流れに限られ、物体後流、境界層などは厳密には平行流ではない（図２）。
（注4）
　撹乱方程式のスペクトル解析において、作用素が非正規のとき一般にはその固有関数は互いに直交しない。その場合、固有値がすべて時間的に減衰する解に対応する場合でも、それらの固有関数の組み合わせによっては過渡的に代数的な増幅を示す場合がある。特に初期撹乱がある程度の大きさをもつとき、この代数的な過渡成長が乱流への遷移に影響を与える可能性が生じる。
（注3）
　流れが不安定であるとき、そこに（時間・空間的に）局所的な微小撹乱を与えると、それは時間とともに増幅する。それが流れとともに移動していく場合を対流不安定、その場に留まる場合を絶対不安定と呼ぶ。
（注2）
　固体、液体、気体などの互いに異なる状態もしくは互いに混じり合わない複数の物質（それぞれの状態・物質を相と呼ぶ）が混在する流れを混相流という。相の境界には界面が存在し、また温度や圧力の変化によって（固体から液体（融解）、液体から気体（沸騰）などの）相転移が生じるが、これらが流れと相互作用して非常に複雑な様相を示すことになる。ビールを注いだ時の流れ（気液二相流）、掃除機でゴミを吸い込む時の流れ（固気二相流）など身の回りにも混相流の例はいたるところに見られる。
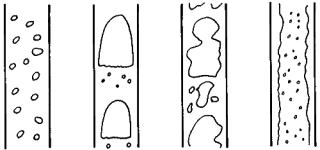
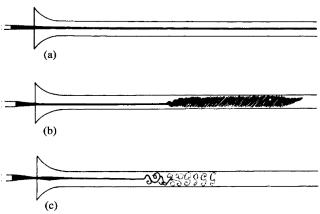　　O. Reynolds (1883) Philos. Trans. 174, 935-982.
(注1)
　Osborne Reynoldsは（極力乱れが入り込まないように注意深く設定した）円管内の流れに染料を注入し、その様子を調べた（右図参照）。流速、管径、温度（粘性・密度）を変化させると、Reynolds数（＝密度×流速×管径/粘性）と呼ばれる無次元数が十分小さいときには染料はきれいな直線を描く（右図(a)）が、Reynolds数を徐々に増加させると、途中から乱れて染料が管内全体に広がるようになる（右図(b)）ことが観測された。
　これは、Reynolds数が大きくなると、直線状の整った流れ（層流）は不安定になり、乱れた流れ（乱流）に遷移するようになることを示している。